Day3 - MySQL 用什麼結構儲存資料？為什麼？(B+Tree & Page)

17th鐵人賽

vicxu

2025-09-03 08:03:23

61 瀏覽

分享至

Tablespace 除了管理 extent 外，也負責將抽象化結構映射到硬碟區塊，因此 extent 中的資料不能亂儲存，要有特定資料結構優化插入查詢的效能，以及特定格式將 bytes 內容解析成帶有欄位意義的資料。

例如下面的 shell script 實作了一個簡單的 key-value 資料庫：

db_set () {  
  echo "$1,$2" >> database  
}  
  
db_get () {  
  grep "^$1," database | sed -e "s/^$1,//" | tail -n 1  
}

資料格式用 , 隔開，前面為 key 後面為 value，而資料結構採用 append-only 的陣列，新增或修改資料是不斷檔案後面插入新一筆紀錄，插入資料雖然很快 O(1) ，但查詢卻要從檔案第一行找到最後一行 O(N)。

那麼 MySQL 用什麼結構儲存資料？

MySQL 設計目的是要能符合頻繁查詢和寫入的情境，因此需要查詢 & 寫入時間複雜度都不能太差的結構。

首先，要從大量資料中查詢單筆資料，最快非 Binary Search 莫屬，但用 Bianry Search 資料需要有序，若用有序陣列，每次插入需要移動陣列元素，並不高效，而 Binary Search Tree (BST) 插入時只要找到位置後修改指標內容，複雜度為 O(LogN)。

但如果有序插入到 BST，會把 Binary Tree 變成 Linked List，插入搜尋會變 O(N)，因此要用平衡 BST (e.g AVL Tree) 確保不論如何插入資料，左右子樹高最多差 1 ，雖然插入會多一個旋轉的操作，但插入和查詢複雜度都為 O(LogN)，是查詢跟寫入都不會太差的結構。

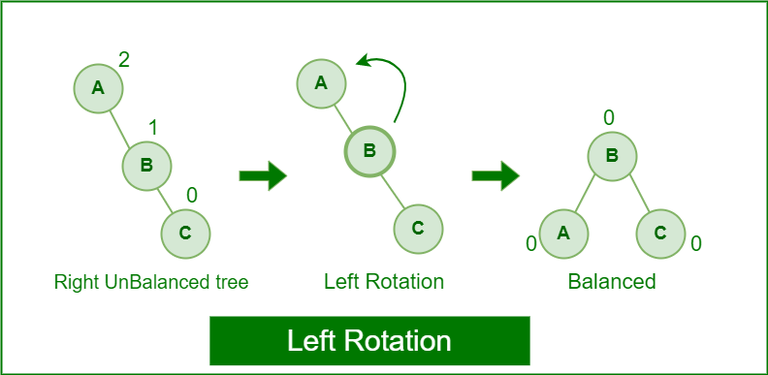
(圖片來源：https://ithelp.ithome.com.tw/m/articles/10353866)

但 MySQL 卻是用 B+Tree 而不是 AVL Tree，為什麼？

AVL Tree 雖儲存在硬碟中，但 Traversal 時要把節點讀到記憶體解析後才能往下個節點找，因此節點越多讀取 I/O 次數越多，優化方式是一次讀取多個節點 (i.e Sub Tree)，但前提要用連續硬碟空間儲存多個節點。

而 B+Tree 正是將多個有序資料壓縮成一個節點且葉節點彼此左右相連的平衡 BST ，B+Tree 的節點稱為 Page 預設為 16 KB 的連續硬碟空間，Treversal 時一次 I/O 能讀到多筆資料，有效降低 I/O 次數。

B+Tree 中間點分裂有啥缺點？

B+Tree 在插入時需要處理節點 (Page) 塞滿的情況，一旦塞滿需要將節點資料分裂出去，傳統做法是從中間點分裂，將左半部跟右半部資料分成兩個子節點，中間值放到父節點：

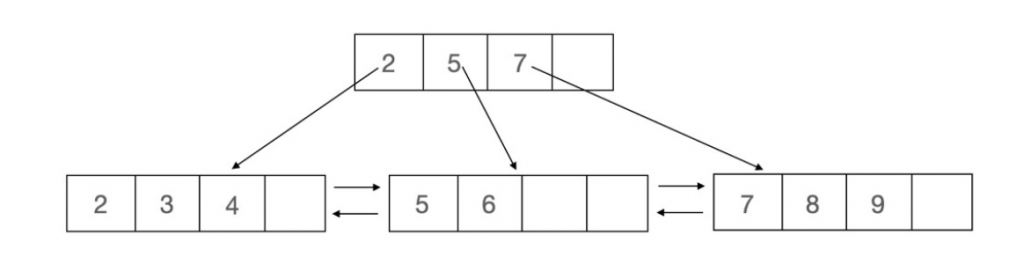
(圖來源：http://mysql.taobao.org/monthly/2021/06/05/)

然而該分裂法在順序插入時，會導致多數節點都處於半滿的情況，可用 https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html 模擬順序插入。

因此 MySQL 採用插入點分裂，需要分裂時檢查新資料是否為節點中的最大或最小值，如果是最大值嘗試將新資料放到右邊子節點，如果右邊子節點不存在就建立一個新節點存放新值，反之亦然，該方法能確保順序插入時，每個節點幾乎全滿。

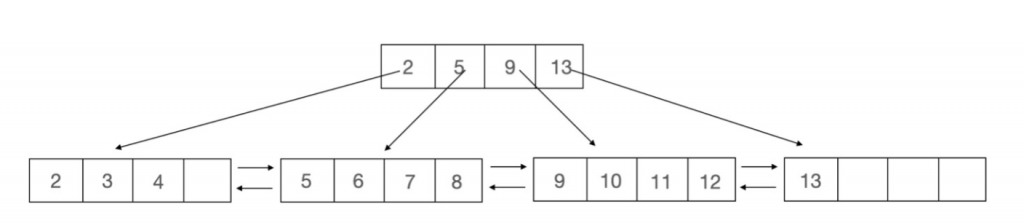
(圖來源：http://mysql.taobao.org/monthly/2021/06/05/)

那麼 B+Tree 節點 (Page) 裡的結構為何呢？

直覺判斷 Page 裡應該是一個 AVL Tree，但不是，原因是 AVL Tree 有多個指標和要記錄樹高，佔用較多空間，Page 結構目的是塞越多資料越好，盡可能降低 Traversal 時的 I/O 次數，因此結構更像是有序陣列。

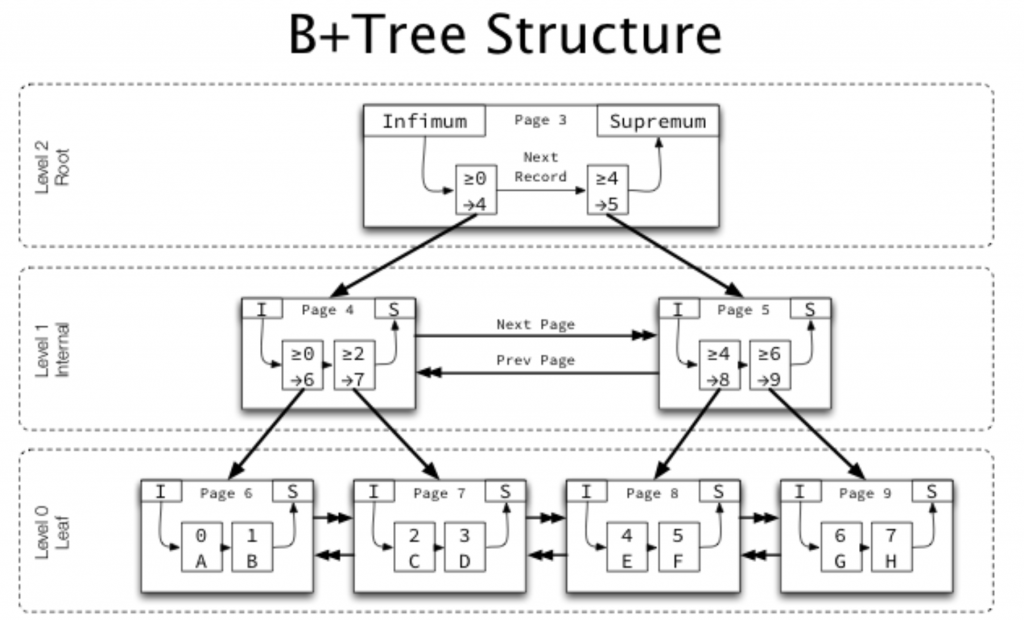
(圖片來源：https://blog.jcole.us/2013/01/10/btree-index-structures-in-innodb/)

但用序陣列的話，插入資料到 Page 效能不就變差了嗎？

讓我們來看下實際的 Page 結構吧！

|header|infimum|supremum|data1|data2|...|free space|page directory|tailer|

上面為 Page 結構內容包含：

header：紀錄 Page Metadata 例如 ID，指向 Child & Sibling Node 的指摽，Page Type (Leaf or Non-Leaf) ，最後更新的 LSN 以及 Free Space 大小等。
infimum (無窮小紀錄) & supremum (無窮大紀錄)：幫助在進行 Binary Search 時不用處理超出陣列邊界的情況，碰到無窮小或無窮大代表資料不在 Page 中。
data：實際儲存資料的地方，是以 row-based 的方式儲存，例如 |column_a|column_b|column_c|，欄位順序為 Table Schema 宣告順序。
free space：可放新資料的空間。
tailer : 用來效驗資料更新是否完整寫入，例如 header 的 LSN 跟 tailer LSN 不一樣代表資料沒完整更新。

最後 page directory 就是讀寫優化的關鍵結構。

新增資料時，會直接放進 Free Space，不會維持有序陣列，也就是說 |data1|data2| 不是有序的，無法 Binary Search，雖然插入變快了，但查詢怎麼辦？

資料在硬碟空間裡雖不是物理有序的，但可用指標 (file offset) 指向下筆紀錄，建立有序的 linked list，不過每次插入都要 scan 整個 linked list O(N) 找到有序的位置，插入效能又變差了，因此需要 page directory！

什麼是 Page directory？

page directory 為一個稀疏索引的有序陣列，該陣列不儲存所有資料，陣列 item 又稱為 slot 儲存某段範圍的最小值的指標 (file offset)，例如 1->2->3->4->6 的有序 linked list，可建立一個 slot 為 2 的 page directory [1,3,6]，當插入 (5) 到 free space 後，可透過 page directory [1,3,6] 陣列進行 Binary Search 找到 3 ，並透過指摽往後找，直到遇到第一個比 (5) 大的資料後插入，變成
1->2->3->4->5->6，此時維持有序的 linked list 時間複雜度就變成 O(LogN+K)，K 為 slot 範圍長度。

page directory 為稀疏的有序陣列大小可控，slot 範圍會根據插入情況動態調整，且不一定每次插入都要搬移資料，插入不會因此變太慢。

從 Page 中查資料時，也可用 page directory 縮小查詢範圍，找出 linked list 搜尋起點在往後查詢，時間複雜度為 O(LogN+K)，整體概念有點像只有兩層的 Skip List。

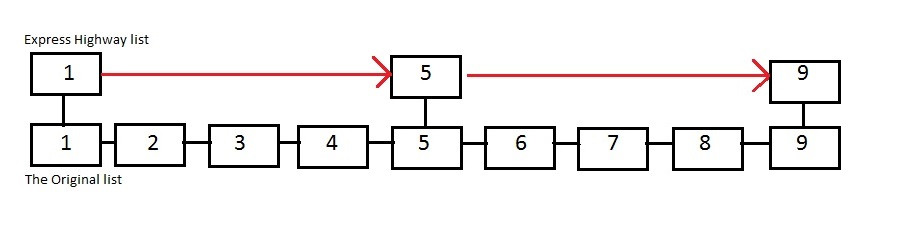
(圖來源:https://parallelcomputing2017.wordpress.com/2017/04/17/skip-list/)